حل یک مسئله 200 ساله جبر توسط ریاضی‌دان استرالیایی
نورمن وایلدبرگر، ریاضی‌دان دانشگاه نیو ساوت ولز استرالیا موفق شده است با راه‌حلی جدید یک مسئله 200 ساله جبر را حل کند. به گزارش تک‌ناک، مسئله‌ای که به حل معادلات چندجمله‌ای با درجه بالا مربوط می‌شود و نزدیک به دو قرن، ذهن ریاضی‌دانان را به خود مشغول کرده بود. این پژوهش با همکاری دین روبین، […] نوشته حل یک مسئله 200 ساله جبر توسط ریاضی‌دان استرالیایی اولین بار در تک ناک - اخبار تکنولوژی روز جهان و ایران. پدیدار شد.
نورمن وایلدبرگر، ریاضی‌دان دانشگاه نیو ساوت ولز استرالیا موفق شده است با راه‌حلی جدید یک مسئله 200 ساله جبر را حل کند.
به گزارش تک‌ناک، مسئله‌ای که به حل معادلات چندجمله‌ای با درجه بالا مربوط می‌شود و نزدیک به دو قرن، ذهن ریاضی‌دانان را به خود مشغول کرده بود.
این پژوهش با همکاری دین روبین، دانشمند علوم رایانه انجام شده و جزئیات آن در قالب یک مقاله منتشر شده است. نویسندگان در این مقاله نشان داده‌اند که چگونه می‌توان این محاسبات پیچیده را با استفاده از رویکردی نوین و بر پایه اعداد کاتالان انجام داد.
اعداد کاتالان دنباله‌ای مشهور در ترکیب‌شناسی هستند، که برای شمارش ساختارهای گوناگون ریاضیاتی، مانند نحوه تقسیم یک چندضلعی به مثلث‌ها یا آرایش صحیح پرانتزها در یک عبارت ریاضی، کاربرد دارند.
وایلدبرگر در توضیح اهمیت این دستاورد برای حل یک مسئله 200 ساله جبر گفت: «این یک بازنگری اساسی در یکی از فصل‌های بنیادین علم جبر است.»
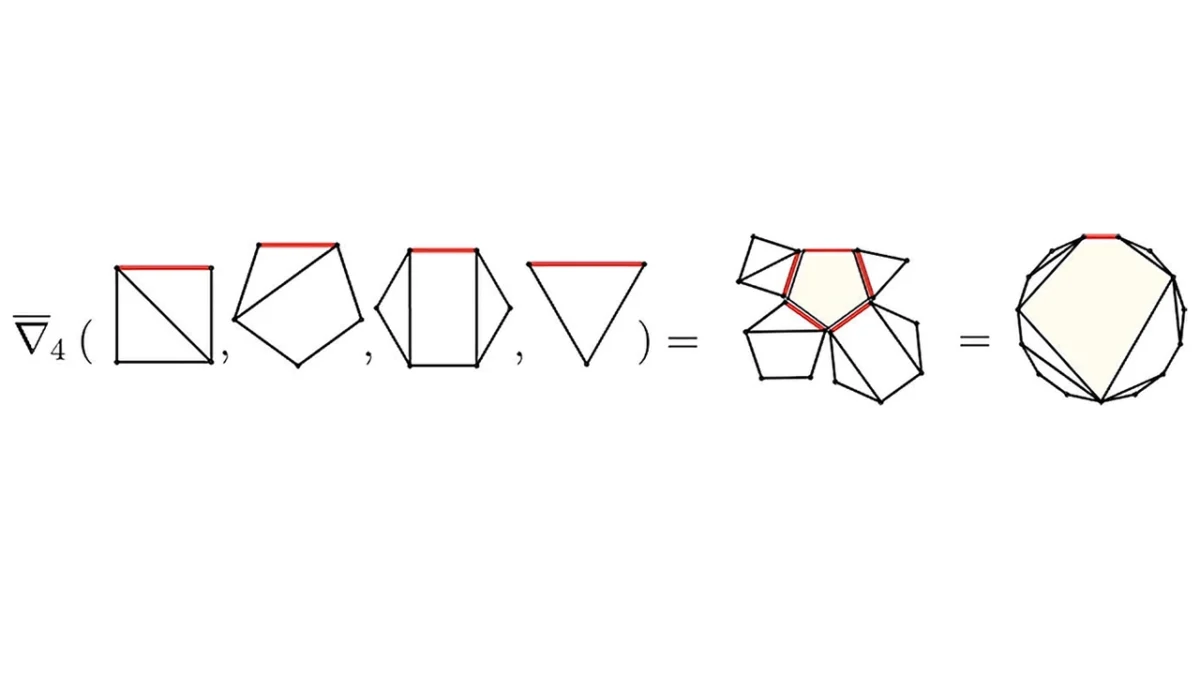
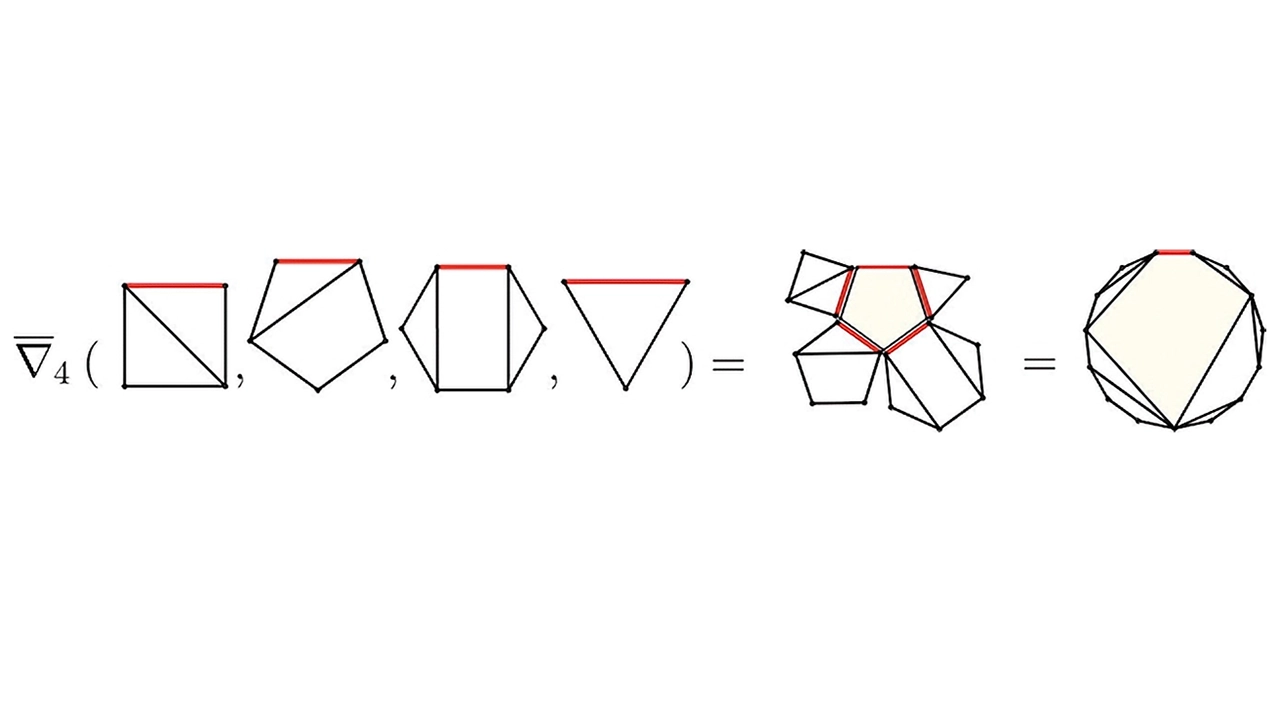
چندجمله‌ای‌ها، معادلاتی هستند که متغیرهایی با توان‌های صحیح و غیرمنفی دارند. زمانی که توان متغیر پنج یا بیشتر باشد، معادله در دسته چندجمله‌ای‌های با درجه بالا قرار می‌گیرد. تاکنون راه‌حل دقیقی برای این معادلات وجود نداشت و متخصصان تنها به پاسخ‌های تقریبی بسنده می‌کردند. اما حالا پژوهشگران موفق شده‌اند که روشی دقیق برای حل آنها ارائه کنند.
وایلدبرگر و روبین در حل مسئله 200 ساله جبر، با کنار گذاشتن روش‌های کلاسیک مبتنی بر رادیکال‌ها (مانند ریشه دوم یا سوم)، به ترکیب‌شناسی روی آوردند؛ شاخه‌ای از ریاضیات که به شمارش الگوهای مختلف می‌پردازد. آنها با گسترش مفهوم اعداد کاتالان — که در شمارش حالات تقسیم چندضلعی‌ها به مثلث‌ها کاربرد دارند — موفق شدند این ایده را به حل معادلات چندجمله‌ای تعمیم دهند.
وایلدبرگر در این‌باره توضیح داد: «اعداد کاتالان ارتباط نزدیکی با معادلات درجه دوم دارند. نوآوری ما در این است که اگر می‌خواهیم معادلات با درجه‌های بالاتر را حل کنیم، باید به دنبال هم‌ارزهای پیشرفته‌تری از این اعداد باشیم.»
این روش جدید روی چند معادله معروف، از جمله یکی از معادلات درجه سوم مورد مطالعه جان والیس، آزمایش شد و نتایج به‌دست‌آمده، صحت آن را تأیید کردند.
همچنین پژوهشگران در جریان این مطالعه، ساختار ریاضی تازه‌ای به نام Geode را کشف کردند، که با اعداد کاتالان در ارتباط است و می‌تواند به عنوان پایه‌ای برای تحقیقات آینده به‌کار رود.
به گفته نویسندگان، این روش می‌تواند مسیر تازه‌ای را برای بازنگری در بسیاری از مفاهیم رایج در ریاضیات، الگوریتم‌های رایانه‌ای، ساختار داده‌ها، نظریه بازی‌ها و حتی زیست‌شناسی باز کند. برای نمونه می‌تواند در محاسبه نحوه تا شدن مولکول‌های RNA مورد استفاده قرار گیرد.
وایلدبرگر در پایان تأکید کرد: «این محاسبه، در قلب بسیاری از کاربردهای ریاضیات قرار دارد و می‌تواند باعث بهبود الگوریتم‌ها در حوزه‌های متعددی شود.»
نوشته حل یک مسئله 200 ساله جبر توسط ریاضی‌دان استرالیایی اولین بار در تک ناک - اخبار تکنولوژی روز جهان و ایران. پدیدار شد.
واکنش شما چیست؟
